ДРОБИ В МАТЕМАТИКЕ
Простой калькулятор дробей
Вычисление производится автоматически — просто заполните ячейки. После калькуляции вы сможете посмотреть решение по действиям, нажав на соответствующую ссылку.
Скрыть подробности
+
=
0
Калькулятор сокращения дробей
Сокращение производится автоматически — просто заполните ячейки. После сокращения вы сможете посмотреть решение по действиям, нажав на соответствующую ссылку.
Скрыть подробности
=
0
Калькулятор приведения дробей к общему знаменателю
Приведение к общему знаменателю производится автоматически — просто заполните ячейки дробей. После выполнения операции вы сможете посмотреть решение по действиям, нажав на соответствующую ссылку.
Скрыть подробности
Ячейки для заполнения
и
Приведенные дроби
0
и
0
Расширенный калькулятор дробей
Вычисления производятся автоматически — просто заполните поле ввода. Расширенный калькулятор позволяет производить арифметические операции с дробными выражениями различной сложности.
Для добавления обыкновенной дроби используйте кнопку:
Для добавления смешанной дроби используйте кнопку:
Скрыть подробности
Начните вводить пример
(
)
÷
×
-
+
7
8
9
4
5
6
1
2
3
00
0
.
Примеры с дробями
1
2
+
3
2
+
5
2
=
2
5
12
7
12
+
5
3
=
2
1
4
2
1
3
+
2
5
+
3
2
=
4
7
30
7
15
+
4
9
=
41
15
4
1
9
+
5
2
9
=
9
1
3
2
5
+
8
3
=
3
1
15
Как проверить домашку по математике без чьей-либо помощи?🤫
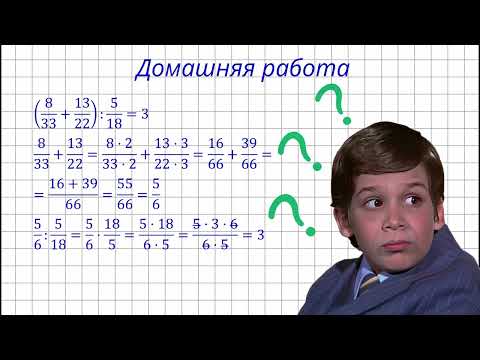
Что такое дроби. Виды дробей
Обыкновенная дробь
Дробь — одна или несколько частей целого. Обыкновенные дроби записывают двумя натуральными числами, разделенными чертой.
В такой записи число a, записанное над чертой, называют числителем, а число b, записанное под чертой, — знаменателем. Знаменатель показывает, на сколько равных частей разделили целое. Числитель показывает, сколько таких частей взяли.
Подробно разбираем в уроке:
Смешанное число
Смешанное число — число, содержащее целую часть и дробную часть, причем дробная часть должна быть правильной дробью.
Неправильную дробь можно перевести в смешанное число, выделив целую часть, а смешанное число можно представить в виде неправильной дроби.
Подробно разбираем в уроке:
Основное свойство дроби
Основное свойство дроби звучит так: если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля, то получится равная ей дробь. Благодаря основному свойству, дроби можно привести к общему знаменателю, умножив числитель и знаменатель на натуральное число, или сократить, разделив числитель и знаменатель на натуральное число.
Подробно разбираем в уроке:
Правила вычислений с дробями
Дроби и смешанные числа можно, так же как и целые числа, складывать, вычитать, умножать и делить. Ниже приведены правила, руководствуясь которыми можно это сделать.
Приведение дробей к общему знаменателю
Чтобы привести дроби к общему знаменателю, надо:
1
найти наименьшее общее кратное знаменателя, то есть наименьший общий знаменатель;
2
найти дополнительный множитель для каждой дроби, разделив наименьший общий знаменатель на знаменатель данной дроби;
3
числитель и знаменатель каждой дроби умножить на соответствующий дополнительный множитель.
Подробно разбираем в уроке:
Сокращение дробей
Чтобы сократить дробь, надо:
1
найти наибольший общий делитель числителя и знаменателя дроби;
2
поделить числитель и знаменатель дроби на данный наибольший общий делитель;
3
числитель и знаменатель каждой дроби умножить на соответствующий дополнительный множитель.
Подробно разбираем в уроке:
Сложение дробей и смешанных чисел
Чтобы сложить дроби или смешанные числа, надо:
1
отдельно сложить целые части (в обыкновенной дроби целая часть равна 0);
2
привести дробные части к общему знаменателю, если необходимо;
3
сложить дробные части;
4
если дробная часть суммы оказалась неправильной дробью, то выделить в ней целую часть и прибавить ее к целой части суммы. Для этого надо:
- числитель поделить на знаменатель с остатком;
- частное от деления прибавить к целой части, полученной на шаге 1, а остаток от деления оставить в числителе дробной части;
5
сократить дробную часть, если необходимо.
Подробно разбираем в уроке:
Вычитание дробей и смешанных чисел
Чтобы найти разность дробей или смешанных чисел, надо:
1
привести дроби, либо дробные части в случае вычитания смешанных чисел, к общему знаменателю, если необходимо. Для этого надо:
- найти наименьшее общее кратное знаменателей, то есть наименьший общий знаменатель;
- найти дополнительный множитель для каждой дроби, разделив наименьший общий знаменатель на знаменатель данной дроби;
- числитель и знаменатель каждой дроби умножить на соответствующий дополнительный множитель.
2
если числитель дробной части уменьшаемого меньше дробной части вычитаемого, занять единицу от целой части уменьшаемого. Для этого целую часть уменьшаемого уменьшить на 1, а числитель дробной части увеличить на число, равное знаменателю дробной части;
3
из целой части уменьшаемого вычесть целую часть вычитаемого;
4
из дробной части уменьшаемого вычесть дробную часть вычитаемого;
5
сократить дробную часть, если необходимо. Для этого надо поделить числитель и знаменатель на наибольший общий делитель числителя и знаменателя.
Подробно разбираем в уроке:
Умножение дробей и смешанных чисел
Чтобы умножить дроби или смешанные числа, надо:
1
перевести смешанные числа в неправильные дроби, если необходимо. Для этого:
- целую часть умножить на знаменатель дробной, прибавить к ней числитель дробной части, и сумму записать в числитель неправильной дроби;
- знаменатель оставить тем же.
2
перемножить числители и записать в числитель произведения, перемножить знаменатели и записать в знаменатель произведения;
3
если в результате получилась неправильная дробь, то выделить целую часть. Для этого:
- числитель поделить на знаменатель с остатком;
- частное от деления записать в целую часть, остаток – в числитель дробной части, знаменатель оставить тем же.
4
сократить дробную часть, если необходимо. Для этого надо поделить числитель и знаменатель на наибольший общий делитель числителя и знаменателя.
Подробно разбираем в уроке:
Деление дробей и смешанных чисел
Чтобы найти частное дробей или смешанных чисел, надо:
1
перевести смешанные числа в неправильные дроби, если необходимо. Для этого:
- целую часть умножить на знаменатель дробной, прибавить к ней числитель дробной части, и сумму записать в числитель неправильной дроби;
- знаменатель оставить тем же.
2
умножить дробь – делимое на дробь, обратную дроби – делителю. Для этого в дроби – делителе поменять числитель и знаменатель местами;
3
если в результате получилась неправильная дробь, то выделить целую часть. Для этого:
- числитель поделить на знаменатель с остатком;
- частное от деления записать в целую часть, остаток – в числитель дробной части, знаменатель оставить тем же.
4
сократить дробную часть, если необходимо. Для этого надо поделить числитель и знаменатель на наибольший общий делитель числителя и знаменателя.
Подробно разбираем в уроке:
Отвечаем на вопросы
Простые дроби (то же, что обыкновенные) — число, представляющее собой одну или несколько частей целого и записанное двумя натуральными числами, разделенными чертой. В противоположность смешанной дроби, дробь, содержащая лишь числитель и знаменатель, называется простой.
Правильная дробь — дробь, у которой числитель меньше знаменателя. Примеры правильных дробей: 1/8, 3/16, 2/9. Неправильная дробь — дробь, у которой числитель равен или больше знаменателя. Примеры неправильных дробей: 8/8, 12/10, 10/10, 15/4.
Взаимно обратные дроби — две дроби, обладающие тем свойством, что числитель первой является знаменателем второй, а знаменатель первой является числителем второй.
Взаимно обратные дроби — две дроби, обладающие тем свойством, что числитель первой является знаменателем второй, а знаменатель первой является числителем второй.
Вычисления в калькуляторе производятся автоматически — просто заполните поле ввода. После калькуляции вы сможете посмотреть решение по действиям, нажав на соответствующую ссылку. Расширенный калькулятор позволяет производить арифметические операции с дробными выражениями различной сложности.
Десятичная дробь — это дробь со знаменателем 10, 100, 1000 и т.д.
Десятичная дробь имеет свою запись, которая называется десятичной. В такой записи запятая отделяет целую часть числа от дробной. Запись дробной части десятичной дроби содержит столько цифр, сколько нулей в записи знаменателя соответствующей обыкновенной дроби.
Например,
3
4
10
3.4
37
1000
0.037
Положительной называется любая дробь, которая больше 0. Обычно они пишутся без знака, но могут иметь знак «+», который пишется перед дробью. Его наличие необязательно, поэтому и— это две записи одного и того же числа., , +
7
9
+
7
9
Например,
3
8
3
7
11
5
6
Отрицательной дробью называется любая дробь, которая имеет значение меньше 0. Такие дроби всегда записываются с помощью знака «–».
Например,
- , , -
7
11
-0.6
3
100
Дробь можно возводить в степень. По правилу умножения дробей, дробь, возведенная в натуральную степень, равна дроби, в которой числитель и знаменатель возведены в эту самую натуральную степень:
(
a
b
)
c
a
b
a
b
c множителей
=
a
c
b
c
Например,
(
4
5
)
3
4
3
5
3
64
125
Дробной степенью называют степень с дробным показателем, то есть любое число, возведенное в степень вида
m
n
Например,
3
5
8
5
8
10
2
3
2
3
Степень с дробным показателем представляет собою корень, показатель которого равен знаменателю дроби, а подкоренное выражение — это степень с тем же основанием, и показателем, равным числителю дроби:
a
m
n
m
n
=
n
a
m
Например,
9
3
2
3
2
=
2
9
3
=
2
729
27
Сообщество
инициативных родителей
Присоединяйтесь к нашему сообществу — тут мы пишем новости
и интересности в сфере образования, а также делимся идеями
и появлением новых разделов на сайте. А еще с упоением читаем
ваши комментарии. 🧡
Все продукты СлонУма
Чтобы пройденная тема стала навыком, каждому требуется изучить разный объем теории и решить разное количество заданий. Через эту призму мы и пропускаем наши обучающие продукты.
Математика
Дроби: теория + практика
15 уроков с видео, 35 тренажеров, сборники задач — освойте все виды дробей в 5-6 классах.
Олимпиада прямо сейчас
Соревнуйтесь в решении задач на логику и счет! Запускаем олимпиаду по математике для учеников 1–8 классов со всей России.
Бесплатные олимпиадные задачи
Олимпиадные задания по математике 1–8 классов — решите 25 увлекательных задач бесплатно.
Задача недели
Каждую неделю вас ждет бесплатная олимпиадная задача по математике + разбор решения предыдущей.
Марафон олимпиадных задач
Решайте 10 заданий в неделю и соревнуйтесь за звание чемпиона с учениками со всей России.